Labyrinthe ?

Le terme labyrinthe vient du grec λαβύρινθος, (en latin labyrinthus), mot dont l’étymologie est douteuse...
Il désigne dans la mythologie grecque une série complexe de galeries construites par Dédale pour enfermer le Minotaure.

 [1]

Par extension, un labyrinthe est un tracé sinueux, muni ou non d’embranchements, d’impasses et de fausses pistes, destiné à perdre ou à ralentir celui qui cherche à s’y déplacer.

Ce motif, apparu dès la préhistoire, se retrouve dans de très nombreuses civilisations sous des formes diverses.

De nos jours, le terme de labyrinthe désigne une organisation complexe, tortueuse, concrète (architecture, urbanisme, jardins, paysages...) ou abstraite (structures, façons de penser...), où l’homme peut se perdre.

Le cheminement du labyrinthe est difficile à suivre et à saisir dans sa globalité.

 Le Labyrinthe... un jeu ?

 [2]

Le concept du labyrinthe a été exploité tout d’abord sous le nom de jeu de l’oie, puis sous celui de Labyrinthe. Depuis quelques années les jeux vidéos tels que Tomb Raider ou encore simplement labyrinthe exploitent ces figures complexes.

De même, le pavillon du Labyrinthe était l’une des plus spectaculaires attractions grandeur nature de l’Exposition universelle de 1967 de Montréal, et comportait des innovations de projection d’images voisines de celles qui seront mises en place bien plus tard dans le Futuroscope.

Le mythe de Dédale et du labyrinthe sont aussi un des quatre mythes fondateurs du Tarot : celui des différentes étapes du voyage initiatique vers la connaissance de soi.

À Londres, un labyrinthe de carreaux de céramique est visible sur le mur de la station de métro Warren Street (warren désigne en anglais les terriers de lapins et leurs dédales de galeries).
Aux heures de pointe, les voyageurs ont deux minutes d’attente en moyenne entre deux trains. L’auteur du dédale a estimé qu’il fallait environ trois minutes pour le résoudre.

 Labyrinthes parfaits et labyrinthes à îlots

Un labyrinthe est une surface connexe.
De telles surfaces peuvent avoir des topologies différentes : simple, ou comportant des anneaux ou îlots.

Ces deux surfaces ne sont topologiquement pas équivalentes.

Cette différence, rapportée aux labyrinthes, conduit à une distinction en deux catégories :

  • celle des labyrinthes dits « parfaits » où un chemin unique passe par toutes les cellules
  • celle des labyrinthes dits « imparfaits » où un chemin se recoupant forme des ensembles de cloisons connexes appelés « îlots ».
    Ces îlots peuvent éventuellement isoler des cellules qui deviennent alors inaccessibles.

 Notions de chemin dans un labyrinthe

Les chemins des labyrinthes parfaits peuvent être représentés par des graphes directs acycliques (ou DAG) :

  • Un labyrinthe parfait et son DAG associé (en rouge). Les noeuds sont marqués selon qu’il s’agit d’entrées ou de sorties, d’intersections ou de cul-de-sac :
  • Vue du DAG précédent déployé en arborescence :

 Recherche de chemins dans un labyrinthe

La recherche de chemin, couramment appelée pathfinding, est un problème de l’intelligence artificielle qui se rattache plus généralement au domaine de la planification et de la recherche de solution.
Il consiste à trouver comment se déplacer dans un environnement entre un point de départ et un point d’arrivée en prenant en compte différentes contraintes.

A la base, un problème de pathfinding peut se ramèner à un problème de recherche du meilleur chemin entre deux noeuds dans un graphe.

Sur l’illustration ci-contre, on trouve deux chemins équivalents allant de A à B, dans un environnement à deux dimensions.

Il existe un ensemble d’algorithmes classiques pour résoudre ce type de problème. Toutefois, le pathfinding devient un problème complexe lorsque l’on cherche à prendre en compte diverses contraintes additionnelles (exécution en temps réel, présence d’incertitudes, contrainte de ressources, environnement évolutif, etc).

Deux algorithmes déterministes principaux sont utilisés pour la recherche du plus court chemin dans un graphe du type labyrinthique :

  • L’Algorithme de Dijkstra, qui permet de déterminer le chemin optimal. Il est, par exemple, utilisé pour le routage Internet.
  • L’Algorithme A*, qui est beaucoup plus rapide à condition d’avoir une bonne fonction heuristique, mais qui donne une solution qui n’est pas forcément optimale. En pratique, l’algorithme A* est un bon compromis entre coût calcul et optimalité de la solution.

Ci contre, un exemple d’exécution de l’algorithme A* en environnement 2D discret.

Les cellules rouges forment un chemin qui part de la cellule verte vers la cellule bleue en évitant l’obstacle formé par les cellules grises.

Les nombres indiquent la distance de Manhattan à la cellule de départ en 4-connectivité.

Il existe des algorithmes qui permettent de calculer le plus court chemin de manière contrainte, par exemple par rapport à une courbure du type chemin de Dubins. Ces algorithmes sont développés pour répondre aux problèmes rencontrés en robotique vis à vis des contraintes matérielles.

 Parcourir et Sortir d’un labyrinthe

On sait, de façon pragmatique, que l’on trouve obligatoirement la sortie d’un labyrinthe si on longe systématiquement un mur en le gardant, sans jamais le lâcher, à main droite ou à main gauche.

Cette idée est vérifiée dans le cas d’un labyrinthe parfait, mais elle peut conduire à explorer la totalité du labyrinthe, c’est-à-dire à passer au moins une fois dans toutes les cellules sans exception. Cela correspond à ce que l’on appelle le parcours de l’arbre en profondeur.

Cette ruse a toutefois été déjouée par les concepteurs de labyrinthes, car dans les labyrinthes à îlots, tourner systématiquement à droite, ou systématiquement à gauche, peut conduire à tourner systématiquement en rond.

L’exemple ci-dessus présente un labyrinthe à îlots imbriqués (avec son graphe abstrait associé) où la méthode de la main au mur est inopérante et où il faut passer à des méthodes plus évoluées.

La sortie d’un labyrinthe relève plus généralement de la recherche de chemin dans le graphe du labyrinthe.
On distingue deux cas :

  • Dans le premier cas, on dispose d’une vue globale et on est capable de distinguer sans ambiguïté deux positions. De plus, on sait localiser la sortie.
    On peut alors utiliser toute ces connaissances pour mesurer une distance (par exemple de Manhattan) par rapport à la sortie et déterminer le chemin pour l’atteindre.
  • Le second cas est celui de la vue locale, celle qu’aurait la personne qui serait placée dans le labyrinthe (toute autre perception que les murs avoisinants étant négligée) en une immersion en trois dimensions.
    Cette personne ne dispose alors plus de moyen de distinguer un couloir ou un carrefour d’un autre.
    Dans ce cas, la sortie d’un labyrinthe ne relève guère plus de la chance pure, à moins d’exploiter une mémoire quelconque. L’explorateur peut utiliser ses propres ressources, en retenant les endroits déjà visités, les décisions prises et en dressant une carte au fur et à mesure.
    Il peut aussi marquer l’environnement en notant par exemple les directions déjà explorées aux carrefours. Le fameux Fil d’Ariane est lui-même la trace concrète que Thésée laisse derrière lui au fur et à mesure qu’il s’enfonce dans l’antre du Minotaure.

 Génération d’un labyrinthe

Les algorithmes proposés ici vont s’intéresser aux labyrinthes parfaits, mais quelques adaptations permettent de créer facilement des labyrinthes à îlots.

Ils sont basés sur l’espace discrétisé dont les cellules carrées sont initialement remplies et séparées par des cloisons, selon les quatre directions (nord, sud, est et ouest).

Un labyrinthe rectangulaire parfait de m colonnes par n lignes est un ensemble de m.n cellules reliées les unes aux autres par un chemin unique.

Chaque cellule est reliée à toutes les autres, et ce, de manière unique.

L’équivalence topologique des surfaces connexes simples va nous servir pour affiner notre vision des labyrinthes parfaits. En effet, les deux surfaces connexes de la figure ci-dessous sont équivalentes : chacune a 11 cellules et 10 murs internes (marqués en pointillés).

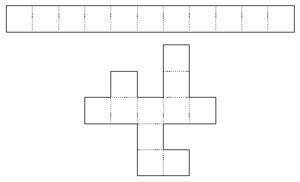
Le nombre de murs ouverts pour permettre un chemin unique dans un labyrinthe de m.n cellules est identique au nombre de murs ouverts pour un chemin droit de m.n cellules, soit (m.n − 1) murs.

Dans un rectangle m.n cellules, le nombre total de murs internes possible est : 2.m.n − m − n.

Pour obtenir ce résultat, on compte deux murs par cellule, par exemple celui du bas et celui de droite (on évite ainsi de recompter deux fois les mêmes) et on retire le nombre de murs limitant le rectangle en bas m et à droite n.

Le nombre de murs fermés dans un labyrinthe parfait est donc de 2.m.n − m − n − (m.n − 1), soit encore (m − 1)(n − 1).

 Algorithme de fusion aléatoire de chemins

Cet algorithme, utilise une propriété des labyrinthes parfaits précédemment énoncée :
Chaque cellule est reliée à toutes les autres, et ce, de manière unique.

Il fonctionne en fusionnant progressivement des chemins depuis la simple cellule jusqu’à l’obtention d’un chemin unique, il suit donc une approche ascendante.

  • L’algorithme associe une valeur unique à chaque cellule (leur numéro de séquence, par exemple) et part d’un labyrinthe où tous les murs sont fermés.
  • A chaque itération, on choisit un mur à ouvrir de manière aléatoire.
  • Lorsqu’un mur est ouvert entre deux cellules adjacentes, les deux cellules sont liées entre elles et forment un chemin.
  • L’identifiant de la première cellule est recopié dans la seconde.
  • À chaque fois que l’on tente d’ouvrir un mur entre deux cellules, on vérifie que ces cellules ont des identifiants différents.
  • Si les identifiants sont identiques, c’est que les deux cellules sont déjà reliées et appartiennent donc au même chemin. On ne peut donc pas ouvrir le mur.
  • Si les identifiants sont différents, le mur est ouvert, et l’identifiant de la première cellule est affecté à toutes les cellules du second chemin.

Au final, on obtient un chemin unique lorsque le nombre de murs ouverts atteint m.n − 1.
Ce qui donne 19 étapes dans l’exemple ci-dessous d’un labyrinthe de 5 x 4 cases :

 Algorithme d’exploration exhaustive de chemins

  • On part d’un labyrinthe où tous les murs sont fermés.
  • Chaque cellule contient une variable booléenne qui indique si la cellule a déjà été visitée ou non (les cellules visitées sont celles qui appartiennent au chemin du labyrinthe en cours de construction).
  • Au départ, toutes les cellules sont marquées comme non visitées (faux).
  • On choisit arbitrairement une cellule et on la marque comme visitée (vrai).
  • Puis on regarde quelles sont les cellules voisines possibles et non visitées et on stocke la position en cours.
  • S’il y a au moins une possibilité, on en choisit une au hasard, on ouvre le mur et on recommence avec la nouvelle cellule.
  • S’il n’y en pas, on revient à la case précédente et on recommence.
  • Lorsque l’on est revenu à la case de départ et qu’il n’y a plus de possibilités, le labyrinthe est terminé.

L’historique des emplacements des cellules précédentes peut être géré de deux façons équivalentes :

  • par la sauvegarde dans un tableau de taille (m.n − 1).
  • par la sauvegarde dans une pile informatique, en utilisant la récursivité.

La formulation récursive donne de très bon résultats pour des labyrinthes de taille modeste.
Dès lors que l’on veut générer de grands labyrinthes (1000 x 1000, par exemple), le programme risque de se terminer brutalement si la taille de la pile est insuffisante (un beau crash et un gel de l’ordinateur). Il est donc important de prévoir une taille de pile suffisante ou à défaut de passer à une autre solution comme l’historique à base de tableau.

L’exploration exhaustive est moins complexe que la fusion de chemins car elle ne nécessite pas la mise en œuvre de structures complexes.

 Comparaison des deux algorithmes retenus

Les deux types d’algorithmes ne sont pas tout à fait équivalents d’un point de vue qualitatif :

  • Le premier type fournit un labyrinthe dont l’arbre est statistiquement mieux équilibré (ou balancé) que celui généré par le second.
    En effet, tous les murs ouvrables ont statistiquement approximativement autant de chances d’être ouverts.
    Le premier algorithme favorisera l’apparition des bifurcations.
  • A contrario, le second privilégie les chemins.
    Les arbres seront donc assez fortement déséquilibrés. Plus un chemin est généré tôt, et plus il a de chances d’être long. Plus il est généré tardivement et plus il a de chances d’être court.
    Le labyrinthe final sera composé de quelques chemins assez longs avec peu de ramifications et les ramifications auront une taille moyenne très inférieure au chemin sur laquelle il se greffe.

Pour des labyrinthes de petite taille, les deux algorithmes donneront des résultats comparables. En revanche, les grands labyrinthes auront des apparences dissemblables.

D’un point de vue quantitatif, le second type d’algorithme sera en moyenne plus rapide que le premier.
Une fois encore, sur de petites surfaces, les temps seront comparables. Mais sur de grandes surfaces, le second se montrera plus performant.

Du point de vue de la mise en œuvre, les deux algorithmes présentés sont probabilistes et à horizon fini, car le nombre de murs à enlever aléatoirement est connu.

En revanche, alors que le premier nécessite une gestion lourde de l’ensemble des murs à considérer, le second est plus simple par sa gestion de l’historique des cellules visitées, il ne requiert pas de traitements lourds et est pleinement déterministe. Il s’impose naturellement comme le meilleur choix possible.

 Représentation d’un labyrinthe au niveau informatique

Choix du modèle de représentation

Le labyrinthe est composé de cellules et de murs.
Ces deux concepts sont équivalents : les cellules sont limitées par des murs et les murs limitent les cellules.
Il nous faut donc choisir lequel de ces deux concepts modéliser.

Étant donné que nous parcourons les pièces (les cases du labyrinthe), il parait plus simple, à priori, de modéliser les cellules plutôt que les murs.

En première approche on pourrait comparer les ouvertures à des passages et de voir les portes comme des pointeurs (des passages) vers d’autres cellules.
Chaque cellule serait composée de 4 pointeurs : une porte serait un pointeur vers une cellule voisine, et un mur un pointeur nul.

Cette démarche fonctionne à merveille, mais si l’on regarde de plus près, nous n’en avons pas besoin.

Nous avons en effet, juste besoin de coder l’état des murs, qui sont soit ouverts, soit fermés.
Il y a 4 portes par cellule, et chaque porte n’a que deux états.
Nous n’avons donc finalement besoin que de quatre informations élémentaires par cellule.

Mais attention, il nous faudra aussi vraisemblablement savoir si nous sommes déjà passés dans une cellule. Ce qui nous rajoute une information supplémentaire par case.

Dans l’absolu, si on réfléchit un peu, cette façon de représenter les données n’est pas très correcte, dans la mesure où l’état d’une porte donnée, est stocké à 2 endroits en même temps : une information dans une cellule, et la même information dans la cellule contigüe.
Pire encore, une porte n’est vraiment ouverte que si elle est ouverte des 2 cotés dans chacune des cases !

Cependant, d’un point de vue pratique, cette redondance ne coûte que très peu (deux informations de trop par cellule), ce qui est d’autant plus négligeable que la taille minimale d’une variable est le caractère (un octet). La redondance du code ouvrant les 2 demi-portes est aussi négligeable en temps de calcul.

Choix de la structure des données

Le labyrinthe en lui même est un ensemble de m.n cellules.
Il nous faut stocker m, n et les cellules elles-mêmes.
Il faut de plus tenir compte de l’entrée et de la sortie du labyrinthe.

L’approche intuitive nous conduit à choisir un tableau de cellules pour représenter toutes les cases et les portes.

Ce n’est peut-être pas la méthode la plus économe en temps de calcul (car il faut passer par des boucles imbriquées) et en place mémoire (un tableau à deux dimensions occupe bien plus de place qu’un vecteur linéaire), mais c’est ce qu’il y a de plus simple au niveau compréhension.

Récapitulons :

  • Un tableau comportant autant de cellules que de cases existantes dans le labyrinthe.
  • Une cellule sera codée sur un caractère (un octet).
  • Les quatres portes seront nommées : Nord, Ouest, Sud et Est.
  • L’état, visité ou non, sera codé dans un tableau parallèle temporaire.

 Implémentation informatique

Les algorithmes présentés peuvent être implémentés et programmés en n’importe quel langage procédural de haut niveau (C, C++, Java, PERL, VBA, etc.).
Le choix s’est porté ici sur du PHP, car facilement accessible et ne nécessitant pas de compilateur, linkeur, et autres usines à gaz à installer avant de pouvoir faire quoi que ce soit...

Ci-après, la définition d’une classe « labyrinthe » regroupant les deux algorithmes de création : méthode par la fusion de chemins et méthode par l’exploration exhaustive de tous les chemins.

<?php

        define('S', 0);                // la direction du sud
        define('E', 1);                // la direction de l'est
        define('N', 2);                // la direction du nord
        define('O', 3);                // la direction de l'ouest
        define('IDX', 3);                // le nombre de directions possibles

class labyrinthe{
        protected $m; // représente la largeur du labyrinthe en cases
        protected $n; // représente la hauteur du labyrinthe en cases
               
        public function __construct($m, $n){
                        $this->m = $m;
                        $this->n = $n;
        }
               
        public function generer_algorithme_de_fusion(){
                $m = $this->m;
                $n = $this->n;
               
                $laby_fusion = array();
               
                // Initialisation du labyrithe
                $k = 0;
                for($i = 0; $i < $n; $i++)
                {
                        $laby_fusion[$i] = array();
                        for($j = 0; $j < $m; $j++)
                        {
                                $laby_fusion[$i][$j] = array();
                                $laby_fusion[$i][$j][S] = 0;
                                $laby_fusion[$i][$j][E] = 0;
                                $laby_fusion[$i][$j][IDX] = $k;
                                $k++;
                        }
                }

                $k--; // On réajuste la variable
               
        $i = 0;
       
        $nb_cloison = ($m*$n)-1;
       
        $murs = array();
       
        for($i = 0; $i < $k; $i++)
        {
                if($i < ($m*($n-1)) )
                        $murs[S][] = $i;
                if(($i+1)%$m)
                {
                        // La case est ouvrable par le mur à droite
                        $murs[E][] = $i;
                }
               
        }
       
        $directions = array(S, E);
                       
        $i = 0;
                while($i < $nb_cloison)
                {
               
                                do{
                                        // On prend n'importe quelle cellule (sauf la dernière qu'on ne peut pas ouvrir)
                                       
                                        // On peut fusionner dans 2 directions S, E
                                        // On en prend une au hasard, si c'est impossible on prend l'autre,
                                        // sinon on prend une autre case.
                                        // On prend une direction au hasard
                                        $dir = $directions[array_rand($directions)];
                                       
                                        // Une case que l'on peut ouvrir dans cette direction
                                        $cle = array_rand($murs[$dir]);
                                        $id = $murs[$dir][$cle];
                                        unset($murs[$dir][$cle]);
                                               
                                        if(empty($murs[$dir]))               
                                                unset($directions[array_search($dir, $directions)]);
                                                       
                                        $x1 = $this->getX($id, $m);
                                        $y1 = $this->getY($id, $m);
                                       
                                        if($dir == S)
                                                $id2 = $id + $m;
                                        else
                                                $id2 = $id +1;
                                               
                                                $x2 = $this->getX($id2, $m);
                                                $y2 = $this->getY($id2, $m);
                                       
                                               
                                                $idx1 = $laby_fusion[$y1][$x1][IDX];
                                                $idx2 = $laby_fusion[$y2][$x2][IDX];
                                               
                                // Tant que l'ouverture rejoint 2 fois le même groupe de cellules
                                }while($idx1 == $idx2);
                               
                       
                                // On ouvre les murs
                                $laby_fusion[$y1][$x1][$dir] = true;
                               
                                // On met les deux cellules au même index
                                for($j = 0; $j < $n; $j++)
                                {
                                        for($k = 0; $k < $m; $k++)
                                        {
                                                if($laby_fusion[$j][$k][IDX] == $idx2)
                                                        $laby_fusion[$j][$k][IDX] = $idx1;
                                        }
                                }
                               
                                $i++;
                               
                }
               
                return $laby_fusion;
        }       

        public function generer_algorithme_par_exploration(){
                        $m = $this->m;
                        $n = $this->n;
                       
                        $laby = array();
                       
                        for($i = 0; $i < $n; $i++)
                        {
                                $laby[$i] = array();
                                for($j = 0; $j < $m;  $j++)
                                {
                                        $laby[$i][$j] = array();
                                        $laby[$i][$j][S] = 0;
                                        $laby[$i][$j][E] = 0;
                                        $laby[$i][$j][IDX] = 0;
                                }
                        }
                       
                        // Pour etre accessible facilement
                        $this->laby = $laby;

                        $x = mt_rand(0, $m-1);
                        $y = mt_rand(0, $n-1);
                       
                        $this->explorer( $x , $y );
                       
                        return $this->laby;
        }       
                       
        private function explorer($x, $y){
                        // En premier temps on cherche les chemin possibles
                        // Si il n'y en a aucun on revoi, sinon on en ouvre un
                        $this->laby[$y][$x][IDX] = 1;
                       
                        $n = $this->n;
                        $m = $this->m;
                       
                        do{
                        // 4 directions possibles N,S,E,O
                        $directions_possibles = array(); // Directions possibles

                        // Au nord
                        if(
                                ($y - 1) >= 0
                                &&
                                $this->laby[$y - 1][$x][IDX] == 0
                        )
                        $directions_possibles[] = N;
                       
                        // Au sud
                        if(
                                ($y + 1) < $n
                                &&
                                $this->laby[$y + 1][$x][IDX] == 0
                        )
                        $directions_possibles[] = S;
                       
                        // A l'est
                        if(
                                ($x + 1) < $m
                                &&
                                $this->laby[$y][$x + 1][IDX] == 0
                        )
                        $directions_possibles[] = E;
                       
                        // A l'ouest
                        if(
                                ($x - 1) >= 0
                                &&
                                $this->laby[$y][$x - 1][IDX] == 0
                        )
                        $directions_possibles[] = O;
                        if(empty($directions_possibles))
                                return;
                               
                        $direction_choisie = $directions_possibles[array_rand($directions_possibles)];
                               
                                if($direction_choisie == N)
                                {
                                        $this->laby[$y - 1][$x][S] = true;
                                        $this->explorer($x, $y-1);
                                }
                                elseif($direction_choisie == S)
                                {
                                        $this->laby[$y][$x][S]  = true;
                                        $this->explorer($x, $y+1);
                                }
                                elseif($direction_choisie == E)
                                {
                                        $this->laby[$y][$x][E] = true;
                                        $this->explorer($x+1, $y);
                                }
                                else{
                                        $this->laby[$y][$x - 1][E] = true;
                                        $this->explorer($x-1, $y);
                                }
                       
                        }while(!empty($directions_possibles));
                        // tant que l'on peut explorer on continue

                        return;
                       
        }       
                       
}
?>

 Labyrinthes interactifs

Et comme un dessin vaut mieux qu’un long discours, vous pouvez jouer avec les modélisations précédentes pour obtenir de délicieuses illustrations de labyrinthes...


Nombre de cases horizontalement
Nombre de cases verticalement
Génération par Fusion  Exploration
Affichage Normal  Ombré
3D
Afficher la solution Oui  Non

Nota  : La méthode par « fusion de chemins » peut prendre jusqu’à plus d’une minute pour la génération d’un labyrinthe... alors soyez un peu patient avant l’obtention de l’image...

P.-S.

D’après un article de Yann Langlais paru dans « LinuxMag France » n°62 en juin 2004.

Notes

[1] Mosaïque romaine de Rhétie représentant le labyrinthe, Thésée et le Minotaure

[2] Labyrinthe digital situé à l’entrée de la cathédrale de Lucques (Toscane, Italie).